 Bishop Hill
Bishop Hill Wilson trending
 Jan 14, 2016
Jan 14, 2016  Climate: MWP
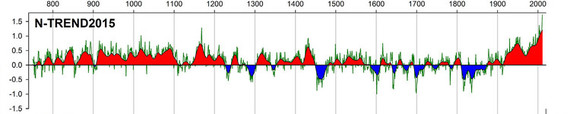
Climate: MWP Rob Wilson emails a copy of his new paper (£) in QSR, co-authored with, well, just about everybody in the dendro community. It's a tree-ring based temperature reconstruction of summer temperatures in the northern hemisphere, it's called N-TREND and excitingly it's a hockey stick!
I gather that Steve McIntyre is looking at it already, so I shall leave it to the expert to pronounce. But on a quick skim through the paper, there are some parts that are likely to prompt discussion. For example, I wonder how the data series were chosen. There is some explanation:
For N-TREND, rather than statistically screening all extant TR [tree ring] chronologies for a significant local temperature signal, we utilise mostly published TR temperature reconstructions (or chronologies used in published reconstructions) that start prior to 1750. This strategy explicitly incorporates the expert judgement the original authors used to derive the most robust reconstruction possible from the available data at that particular location.
But I'd like to know how the selection of chronologies used was made from the full range of those available. Or is this all of them?
If so, there are not many - only 54 at peak. Moreover, the blade of the stick is only supported by a handful. On a whim, I picked one of these series at random - a reconstruction of summer temperatures for Mount Olympus by Klesse et al, which runs right up to 2011. Here's their graph:
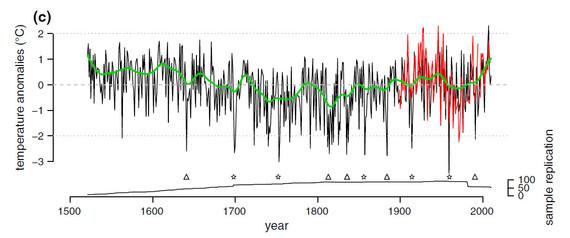 You can see the uptick in recent years, but you can also see an equally warm a medieval warm period. This is only one of the constituent series of course, but I think it will be worth considering this in more detail as it does raise questions over the robustness of the NTREND hockey stick blade.
You can see the uptick in recent years, but you can also see an equally warm a medieval warm period. This is only one of the constituent series of course, but I think it will be worth considering this in more detail as it does raise questions over the robustness of the NTREND hockey stick blade.


Reader Comments (171)
Bloviating, gross extrapolation from minimal data and general speculation abound here. This is not skepticism it is blind naysaying. So how do you find out if something is a 'reliable proxy' or not if you don't screen? The fact is that if local screening had been done on past data then the anomalous bristlecone pines and the single tree from Yamal that were omnipresent in the earlier recons would have been weeded out. There are indeed many things that make some trees good proxies and others bad - even in the same stand (damage, position, etc). It's really isn't too difficult to figure that out even if you don't want to bother reading anything about it.
This is not to deny the 'false positives' issue due to overuse of stats, use of the execrable statistical significance or data-mining by social sciences, epidemiology etc, Sure there is bad practice but there is also good practice. Ljungqvist, as mentioned above (http://onlinelibrary.wiley.com/doi/10.1111/j.1468-0459.2010.00399.x/abstract) was good practice because of the reconciliation of proxies to local temps by screening. The Mannomatic that doesn't recognise upside-down proxies was bad practice because of the abject lack of basic, local screening.
So how do you find out if something is a 'reliable proxy' or not if you don't screen?
======================================
that is simple. take all your samples. randomly select groups of samples and measure them to see how well they track the measure of interest, in this case temperature. in this way you will end up with a normal distribution that you can analyse to see how good a proxy tree rings really are. the ratio of tree rings that do track temperature as compared to tree rings that do not track temperature for example will give you a gross measure of reliability.
However, what you cannot do and must not do is to take ONLY the tree rings that did track temperature and then use ONLY them to do further statistical analysis. Because at that moment you have introduced selection bias into your results and the peer reviewed literature in fields outside of dendroclimatology is rife with examples of how this leads to spurious correlations and misleading results
for example if after sampling you find 10% of tree rings track do track temperature and 90% do not, then you can be pretty sure that tree rings are a useless proxy for temperature and that most of the 10% that do track temperature are false positives. If you were to blindly use this 10% under the mistaken assumption that they were a good proxy for temperature you would end up with bogus results.
If on the other hand, you find that 90% of tree rings do track temperature and only 10% do not, then you could reasonable use the full set of tree rings as a proxy for temperature. However, you still cannot use only the 90% that do track temperature under the assumption that this will improve the accuracy of your result. It will not, because it will amplify the false positives as well as the true positives, again leading to spurious correlations and bogus results.
The magnitude of the error in the 90& case will likely be less than in the 10% case, but in both cases filtering hides the error so you cannot reliably calculate how good a result you have. In both cases the resulting statistics will make your result appear better than it really is.
selection on the dependent variable - aka tree ring calibration
===================
the problem comes down to understanding that statistics relies on assumptions. the primary assumption being that your sample is random and thus representative of the population.
as soon as your "calibrate" (filter) tree rings based on how well they correlate with temperature you no longer have a representative sample. you have violated the underlying assumption of statistics. something you are mathematically forbidden to do. your sample is now biased and it will more than likely lead to spurious (false) correlations and misleading results if it is used in statistical studies of temperature.
every temperature profile based on tree rings should include firstly a study of the quality of the tree rings used as a proxy for temperature. Included should be:
1. a reliability average and deviation should be given for the whole population. ie, how many tree ring samples tracked temperature as compared to those that did not, and what sort of variance was found in this measure.
2. an assurance should be provided that the temperature profile was drawn from the entire sample population, that no temperature related filtering was done to artificially reduce the error.
3. any non-temperature related filtering done to the sample should be subject to sensitivity analysis. for example, if rainfall was known, one might filer based on correlation to rainfall to improve the quality of the population with respect to temperature. this might or might not introduce spurious results, because of possible correlations between rainfall and temperature.
I've re-analysed all 54 datasets for the period 1710-1998, the period where all sets have data. No statistical nonsense was applied. Calculating both the average and standard deviation, there is an interesting result!
For the period 1710 to 1998, there is virtually no change in the 30 year average of the deviation. What this says loud and clear is that there is no evidence in this data for climate change being due to anything other than natural causes. There is no evidence that industrialization is affecting the variability of climate. Otherwise we should be seeing a statistically significant increase in the variance. But we don't.
http://oi64.tinypic.com/4ufho7.jpg
It couldn't be because TREES LIKE ALL PLANTS GROW FASTER IN ATMOSPHERE WITH HIGHER CO2, that the tree-rings are wider as humans put more CO2 into the air?
Using plant growth rate as a proxy for TEMPERATURE ignores the fact that plant growth is directly stimulated by HIGHER CO2 CONCENTRATION independent of TEMPERATURE.
It took me less than thirty seconds to completely discount the temperature validity of this 'study'.
plant growth is directly stimulated by HIGHER CO2 CONCENTRATION independent of TEMPERATURE
================
and given that CO2 is released by a warming ocean, and rainfall increases with a warming ocean, the problem becomes even more complicated. You have a non-linear multivariate problem with auto-correlation and cross-correlation.
but not to worry. we can solves this in excel - NOT! These sorts of problems are on the bleeding edge of mathematics. the results are typically highly sensitive to small changes in the inputs, making an conclusions highly unreliable.
fredberple, what if you say that only some trees are good thermometers? Doesn't that then burden you with establishing how good, one tree at a time which might be done by looking at part of the ring-set for which there is good parallel instrumental data while ignoring another part for which there is also good instrumental data, then with those which qualify on the first look, check for qualification on the second part. those that fail the second check are therefore not good thermometers over the longer period.
I guess I'm suggesting that maybe there's nothing wrong with choosing trees which appear to be thermometers and ignoring ones which aren't and no obligation arises to include the poor with the better. So long as no-one is saying all trees make good thermometers, and I don't see anyone saying that.
This is not to suggest that there may not be other problems here, but the population isn't all trees, it's trees which appear to have this quality.
there's nothing wrong with choosing trees which appear to be thermometers
============================
There most certainly is, if you are going to use statistics to analyse the data.
The problem is well known outside of dendroclimatology. Google "selecting on the dependent variable'.
The trouble is that this is one of those cases where "common sense" is telling you one thing, but mathematics is telling you something else. And since you are using math to analyze the data, you need to obey the rules of math. Statistic says selecting on the dependent variable is forbidden.
it's trees which appear to have this quality.
================================
some of the trees that appear to have this quality actually have this quality. and some of the trees that appear to have this quality don't actually have this quality. the problem is knowing which is which.
and it is the trees that don't appear to have this quality that give you the answer. by removing these trees you make your answer falsely appear more reliable than it actually is. this leads to bogus conclusions.
see my post of Jan 17, 2016 at 2:58 PM.
fredberple, what if you say that only some trees are good thermometers?
========================
trees don't respond linearly to temperature like real thermometers do. Thermometers don't react to CO2 and moisture and soil conditions the way trees do.
So if what you have acts like a good thermometer, I would say you probably don't have a tree at all. what you have is a thermometer.
Ceci n'est pas une pipe.
================
fredberple, suppose you look at it another way. you have a factory which makes liquid thermometers, but the QC isn't good and the bores are not always cylindrical, such that when the temperature measured reaches a level where the bore is bigger, the liquid doesn't rise as much per degree of temperature increase. and when the bore is smaller it rises more - not linear in other words. if they are all different, they would all need the indexes calibrated to agree with the bore condition.
so far so good?
If you pick the best ones, calibrate them against a known standard, even thought the best ones may still not be linear, but at least the indexes are adjusted to compensate, tell me why any analysis of the selected ones has to refer in any way to those rejected
if you are the manufacturer, you would care about the entire population, but if you just want to measure temperature I don't see why you'd give a hoot about the rest of them. I submit that although your criterion that all tree data be referenced in the statistical analysis while necessary for some work is not pertinent to the appraisals of the performance of the population of selected treemometers.
you have a factory which makes liquid thermometers
========================================
ah but that is an entirely different problem statistically, because in the factory you are controlling the environment of the calibration test. you know for CERTAIN that ONLY temperature can be affecting you thermometers during the factory calibration process. There is zero chance of false positives due to other factors.
This is not the case for tree rings. There are many chances for false positives, because trees during the calibration period are being affected by much more than temperature and you have not controlled for these factors.
So you see, that while the problems may appear similar, they are not.
But let me ask you a question. Would you trust the thermometers from a factory with a 90% reject rate and consider it equal to a thermometer from a factory with a 0.01% reject rate?
a factory with a 90% reject rate
==============
given that both factories are using the sale calibrations test, most of us understand that a factory with a 90% reject rate is probably not producing very good thermometers.
so when climate scientists filter their tree ring samples based on temperature, and don't tell us the reject rate, we have no way of knowing statistically how reliable the samples are.
if 99.9% of the tree ring samples passed calibration, then I would agree the remaining 99.9% is likely to be pretty reliable statistically,and we could add back in the 0.01% reject rate to calculate the error term.
if however only 10% of the tree ring samples passed calibration, then I would say this remaining 10% is junk, that most of those 10% simply passed by chance and are false positives and if you try and use them in climate studies they will lead to spurious correlations and bogus results.
Thus, in any statistical study we need to know the size of the original population, not just the size after "calibration". Otherwise we cannot tell if the study is likely to be good or bad.
fredberple, what you have written above is pretty convincing. my analogy has a flaw in its relevance to the tree-rings, which is that the calibration cures the liquid thermometers even if each one is defective in a different way, assuming that a linear scale isn't critical. And the scales could be non-linear in different temperature ranges.
i suspect that tree-rings are not susceptible to this sort of calibration correction, or are they?
I might also suggest that even on 'calibrated' tree-rings, it is a mighty leap to assume that ring data outside the calibrated range is accurate because the data within the calibrated range seems to be. It would also be interesting to learn how many trees which meet calibration for say 1870-1930 flunk 1930-1970. This would certainly give you a feeling for how iffy this whole line is. I don't think these guys are so dense as not to have looked into this in detail.
I've been reading this stuff for 10 years now, but I am pretty dense. I think this particular topic has been hashed out at great length at Steve M's.
Interesting thread - especially the comments from ferdberple and the "naive" questioning by jferguson (reflecting my own lack of knowledge in this area). If ferdberple is correct then it looks like RW and TO are completely undermined. I notice that RW and TO have not ventured any attempt to refute ferdberple's observations.
The factory analogy is flawed. The correct analogy would be to attempt to validate (say) the tube width at only a single limited-length location and assume that it is correct for the entire length of the tube.
I'd like to thank everybody on this thread for a really interesting discussion.
To Rob and Tim, coming here to invite dialogue on your recent initiative. And to Ferd for raising a fundamental concern, explaining it in a straightforward way, as well as patiently answering questions.
I was wondering if this calibration/selection question is a potential explanation for the Divergence Problem? If proxies appear valid over the calibration period, could divergence be "false positives" revealing themselves in later periods?
It would to hear views. Thanks
Bravo JamesSmyth: spot on.
Jeff Id has a post on this paper:
https://noconsensus.wordpress.com/2016/01/16/nearly-two-teams-of-hockey-sticks-used-in-massive-wilson-super-reconstruction/#comments