 Bishop Hill
Bishop Hill Why doesn't the AR5 SOD's climate sensitivity range reflect its new aerosol estimates?
 Dec 19, 2012
Dec 19, 2012  Climate: sensitivity
Climate: sensitivity This is a guest post by Nic Lewis. Please note that comments will be tightly moderated for tone and relevance.
There has been much discussion on climate blogs of the leaked IPCC AR5 Working Group 1 Second Order Draft (SOD). Now that the SOD is freely available, I can refer to the contents of the leaked documents without breaching confidentiality restrictions.
I consider the most significant – but largely overlooked – revelation to be the substantial reduction since AR4 in estimates of aerosol forcing and uncertainty therein. This reduction has major implications for equilibrium climate sensitivity (ECS). ECS can be estimated using a heat balance approach – comparing the change in global temperature between two periods with the corresponding change in forcing, net of the change in global radiative imbalance. That imbalance is very largely represented by ocean heat uptake (OHU).
Since the time of AR4, neither global mean temperature nor OHU have increased, while the IPCC's own estimate of the post-1750 change in forcing net of OHU has increased by over 60%. In these circumstances, it is extraordinary that the IPCC can leave its central estimate and 'likely' range for ECS unchanged.
I focussed on this point in my review comments on the SOD. I showed that using the best observational estimates of forcing given in the SOD, and the most recent observational OHU estimates, a heat balance approach estimates ECS to be 1.6–1.7°C – well below the 'likely' range of 2–4.5°C that the SOD claims (in Section 10.8.2.5) is supported by the observational evidence, and little more than half the best estimate of circa 3°C it gives.
The fact that ECS, as derived using the new aerosol forcing estimates and a heat balance approach, appears to be far lower than claimed in the SOD is highlighted in an article by Matt Ridley in the Wall Street Journal, which uses my calculations. There was not space in that article to go into the details – including the key point that the derived ECS estimate is very well constrained – so I am doing so here.
How does the IPCC arrive at its estimated range for climate sensitivity?
Methods used to estimate ECS range from:
(i) those based wholly on simulations by complex climate models (GCMs), the characteristics of which are only very loosely constrained by climate observations, through
(ii) those using simpler climate models whose key parameters are intended to be constrained as tightly as possible by observations, to
(iii) those that rely wholly or largely on direct observational data.
The IPCC has placed a huge emphasis on GCM simulations, and the ECS range exhibited by GCMs has played a major role in arriving at the IPCC's 2–4.5°C 'likely' range for ECS. I consider that little credence should be given to estimates for ECS derived from GCM simulations, for various reasons, not least because there can be no assurance that any of the GCMs adequately reflect all key climate processes. Indeed, since in general GCMs significantly overestimate aerosol forcing compared with observations, they need to embody a high climate sensitivity or they would underestimate historical warming and be consigned to the scrapheap. Observations, not highly complex and unverifiable models, should be used to estimate the key properties of the climate system.
Most observationally-constrained studies use instrumental data, for good reason. Reliance cannot be placed on paleoclimate proxy-based estimates of ECS – the AR4 WG1 report concluded (Box 10.2) that uncertainties in Last Glacial Maximum studies are just too great, and the only probability density function (PDF) for ECS it gave from a last millennium proxy-based study contained little information.
Because it has historically been difficult to estimate ECS purely from instrumental observations, a standard estimation method is to compare observations of key observable climate variables, such as zonal temperatures and OHU, with simulations of their evolution by a relatively simple climate model with adjustable parameters that represent, or are calibrated to, ECS and other key climate system properties. A number of such ‘inverse’ studies, of varying quality, have been performed; I refer later to various of these. But here I estimate ECS using a simple heat balance approach, which avoids dependence on models and also has the advantage of not involving choices about niceties such as truncation parameters and Bayesian priors, which can have a major impact on ECS estimation.
Aerosol forcing in the SOD – a composite estimate is used, not the best observational estimate
Before going on to estimating ECS using a heat balance approach, I should explain how the SOD treats forcing estimates, in particular those for aerosol forcing. Previous IPCC reports have just given estimates for radiative forcing (RF). Although in a simple world this could be a good measure of the effective warming (or cooling) influence of every type of forcing, some forcings have different efficacies from others. In AR5, this has been formalised into a measure, adjusted forcing (AF), intended better to reflect the total effect of each type of forcing. It is more appropriate to base ECS estimates on AF than on RF.
The main difference between the AF and RF measures relates to aerosols. In addition, the AF uncertainty for well-mixed greenhouse gases (WMGG) is double that for RF. Table 8.7 of the SOD summarises the AR5 RF and AF best estimates and uncertainty ranges for each forcing agent, along with RF estimates from previous IPCC reports. The terminology has changed, with direct aerosol forcing renamed aerosol-radiation interactions (ari) and the cloud albedo (indirect) effect now known as aerosol-cloud interactions (aci).
Table 8.7 shows that the best estimate for total aerosol RF (RFari+aci) has fallen from −1.2 W/m² to −0.7 W/m² since AR4, largely due to a reduction in RFaci, the uncertainty band for which has also been hugely reduced. It gives a higher figure, −0.9 W/m², for AFari+aci. However, −0.9 W/m² is not what the observations indicate: it is a composite of observational, GCM-simulation/aerosol model derived, and inverse estimates. The inverse estimates – where aerosol forcing is derived from its effects on observables such as surface temperatures and OHU – are a mixed bag, but almost all the good studies give a best estimate for AFari+aci well below −0.9 W/m²: see Appendix 1 for a detailed analysis.
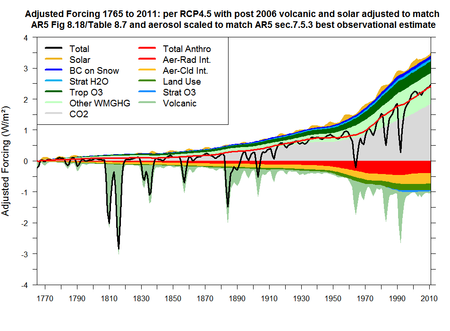
It cannot be right, when providing an observationally-based estimate of ECS, to let it be influenced by including GCM-derived estimates for aerosol forcing – a key variable for which there is now substantial observational evidence. To find the IPCC's best observational (satellite-based) estimate for AFari+aci, one turns to Section 7.5.3 of the SOD, where it is given as −0.73 W/m² with a standard deviation of 0.30 W/m². That is actually the same as the Table 8.7 estimate for RFari+aci, except for the uncertainty range being higher. Table 8.7 only gives estimated AFs for 2011, but Figure 8.18 gives their evolution from 1750 to 2010, so it is possible to derive historical figures using the recent observational AFari+aci estimate as follows.
The values in Figure 8.18 labelled 'Aer-Rad Int.' are actually for RFari, but that equals the purely observational estimate for AFari (−0.4 W/m² in 2011), so they can stand. Only the values labelled 'Aer-Cld Int.', which are in fact the excess of AFari+aci over RFari, need adjusting (scaling down by (0.73−0.4)/(0.9−0.4), all years) to obtain a forcing dataset based on a purely observational estimate of aerosol AF rather than the IPCC's composite estimate. It is difficult to digitise the Figure 8.18 values for years affected by volcanic eruptions, so I have also adjusted the widely-used RCP4.5 forcings dataset to reflect the Section 7.5.3 observational estimate of current aerosol forcing, using Figure 8.18 and Table 8.7 data to update the projected RCP4.5 forcings for 2007–2011 where appropriate. The result is shown below.
The adjustment I have made merely brings estimated forcing into line with the IPCC's best observationally-based estimate for AFari+aci. But one expert on the satellite observations, Prof. Graeme Stephens, has stated that AFaci is at most ‑0.1 W/m², not ‑0.33 W/m² as implied by the IPCC's best observationally-based estimates: see here and slide 7 of the linked GEWEX presentation. If so, ECS estimates should be lowered further.
Reworking the Gregory et al. (2002) heat balance change derived estimate of ECS
The best known study estimating ECS by comparing the change in global mean temperature with the corresponding change in forcing, net of that in OHU, is Gregory et al. (2002). This was one of the studies for which an estimated PDF for ECS was given in AR4. Unfortunately, ten years ago observational estimates of aerosol forcing were poor, so Gregory used a GCM-derived estimate. In July 2011 I wrote an open letter to Gabi Hegerl, joint coordinating lead author of the AR4 chapter in which Gregory 02 was featured, pointing out that its PDF was not computed on the basis stated in AR4 (a point since conceded by the IPCC), and also querying the GCM-derived aerosol forcing estimate used in Gregory 02. Some readers may recall my blog post at Climate Etc. featuring that letter, here. Using the GISS forcings dataset, and corrected Levitus et al. (2005) OHU data, the 1861–1900 to 1957–1994 increase in Q − F (total forcing - OHU) changed from 0.20 to 0.68 W/m². Dividing 0.68 W/m² into ΔT', the change in global surface temperature, being 0.335°C, and multiplying by 3.71 W/m² (the estimated forcing from a doubling of CO2 concentration) gives a central estimate (median) for ECS of 1.83°C.
I can now rework my Gregory 02 calculations using the best observational forcing estimates, as reflected in Figure 8.18 with aerosol forcing rescaled as described above. The change in Q - F becomes 0.85 W/m². That gives a central estimate for ECS of 1.5°C.
An improved ECS estimate from the change in heat balance over 130 years
The 1957–1994 period used in Gregory 02 is now rather dated. Moreover, using long time periods for averaging makes it impossible to avoid major volcanic eruptions, which involve uncertainty as to the large forcing excursions involved and their effects. I will therefore produce an estimate based on decadal mean data, for the decade to 1880 and for the most recent decade, to 2011. Although doing so involves an increased influence of internal climate variability on mean surface temperature, it has several advantages:
a) neither decade was significantly affected by volcanic activity;
b) neither decade encompassed exceptionally large ENSO events, such as the 1997/98 El Nino, and average ENSO conditions were broadly neutral in both decades (arguably with a greater tendency towards warm El Nino conditions in the recent decade); and
c) the two decades are some 130 years apart, and therefore correspond to similar positions in the 60–70 year quasi-periodic AMO cycle (which appears to have a peak-to-peak influence on global mean temperature of the order of 0.1°C).
Since estimates of OHU have become much more accurate during the latest decade, as the ARGO network of diving buoys has come into action, the loss of accuracy by measuring OHU only over the latest decade is modest.
I summarise here my estimates of the changes in decadal mean forcing, heat uptake and global temperature between 1871–1880 and 2002–2011, and related uncertainties. Details of their derivations are given in Appendix 2.
|
Change in global decadal mean between 1871–1880 and 2002–2011 |
Mean estimate |
Standard deviation |
Units |
|---|---|---|---|
|
Adjusted forcing: CO2 and other well-mixed greenhouse gases |
|
0.29 |
W/m² |
|
Adjusted forcing: all other sources (balancing error standard dev.) |
|
0.34 |
W/m² |
|
Adjusted forcing: total |
2.09 |
0.45 |
W/m² |
|
|
|
|
|
|
Earth's heat uptake |
0.43 |
0.08 |
W/m² |
|
|
|
|
|
|
Surface temperature |
0.73 |
0.12 |
°C |
Now comes the fun bit, putting all the figures together. The best estimate of the change from 1871–1880 to 2002–2011 in decadal mean adjusted forcing, net of the Earth's heat uptake, is 2.09 − 0.43 = 1.66 W/m². Dividing that into the estimated temperature change of 0.727°C and multiplying by 3.71 W/m² gives an estimated climate sensitivity of 1.62°C, close to that from reworking Gregory 02.
Based on the estimated uncertainties, I compute a 5–95% confidence interval for ECS of 1.03‑2.83°C – see Appendix 3. That implies a >95% probability that ECS is below the IPCC's central estimate of 3°C.
ECS estimates from recent studies – good ones…
As well as this simple estimate from heat balance implying a best estimate for ECS of approximately 1.6°C, and the reworking of the Gregory 02 results suggesting a slightly lower figure, two good quality recent observationally-constrained studies using relatively simple hemispheric-resolving models also point to climate sensitivity being about 1.6°C:
- Aldrin et al. (2012), an impressively thorough study, gives a most likely estimate for ECS of 1.6°C and a 5–95% range of 1.2–3.5°C.
- Ring et al. (2012) also estimates ECS as 1.6°C, using the HadCRUT4 temperature record (1.45°C to 2.01°C using other records).
And the only purely observational study featured in AR4, Forster & Gregory (2006), which used satellite observations of radiation entering and leaving the atmosphere, also gave a best estimate of 1.6°C, with a 95% upper bound of 4.1°C.
and poor ones…
Most of the instrumental-observation constrained studies featured in IPCC reports that give PDFs for ECS peaking at significantly over 2°C have some identifiable deficiency. Two such studies were featured in Figure 9.21 of AR4 WG1: Forest 06 and Knutti 02. Forest 06 has several statistical errors (see here) and other problems. Knutti 02 used a weak statistical procedure and an arbitrary combination of five ocean models, and there is little information content in its probabilistic ECS estimate.
Five of the PDFs for ECS from 20th century studies featured in Figure 10.19 of the AR5 SOD peak significantly above 2°C:
- one is Knutti 02;
- three are various cases from Libardoni and Forest (2011), a study that suffers the same deficiencies as Forest 06;
- one is from Olson et al. (2012); the Olson PDF, like Knutti 02's, is extremely wide and contains almost no information.
Conclusions
In the light of the current observational evidence, in my view 1.75°C would be a more reasonable central estimate for ECS than 3°C, perhaps with a 'likely' range of around 1.25–2.75°C.
Nic Lewis
Appendix 1: Inverse estimates of aerosol forcing – the expert range largely reflects the poor studies
The AR5 WG1 SOD composite AFari+aci estimate of −0.9 W/m² is derived from mean estimates from satellite observations (−0.73 W/m²), GCMs (−1.45 W/m² from AR4+AR5 models including secondary processes, −1.08 W/m² from CMIP5/ACCMIP models) and an "expert" range of −0.68 to −1.52 W/m² from combined inverse estimates. These figures correspond to box-plots in the lower panel of Figure 7.19. One of the inverse studies cited hasn't yet been published and I haven't been able to obtain it, but I have examined the other twelve studies.
Because of its strong asymmetry between the northern and southern hemispheres, in order to estimate aerosol forcing with any accuracy using inverse methods it is essential to use a model that, at a minimum, resolves the two hemispheres separately. Only seven of the twelve studies do so. Of the other five:
- one is just a survey and derives no estimate itself;
- one (Gregory 02) merely uses an AOGCM-derived estimate of a circa 100-year change in aerosol forcing, without itself deriving any estimate;
- three are based on global-mean only data (with two of them assuming an ECS of 3°C when estimating aerosol forcing).
One of the seven potentially useful studies is based on GCM simulations, which I consider to be untrustworthy. A second does not estimate aerosol forcing over 90S–28S, and concludes that over 1976–2007 it has been large and negative over 28S–28N and large and positive over 28N–60N, the opposite of what is generally believed. A third study is Andronova and Schlesinger (2001), which it turns out had a serious code error. Its estimate of −0.54 to −1.30 W/m² falls to −0.42 to −0.99 W/m² when using the corrected model (Ring et al., 2012). Three of the other studies, all using four latitude zones, estimate aerosol forcing to be even lower: in the ranges −0.14 to −0.74, −0.3 to −0.95 and −0.19 to −0.83 W/m². The final study estimates it to be around or slightly above −1 W/m², but certainly below −1.5 W/m². One recent inverse estimate that the SOD omits is −0.7 W/m² (mean – no uncertainty range given) from Aldrin et al. (2012).
In conclusion, I wouldn't hire the IPCC's experts if I wanted a fair appraisal of the inverse studies. A range of −0.2 to −1.3 W/m² looks more reasonable – and as it happens, is centred almost exactly on the mean of the estimates derived from satellite observations.
Appendix 2: Derivation of the changes in decadal mean global temperature, forcing and heat uptake
Since it extends back before 1880 and includes a correction to sea surface temperatures in the mid-20th century, I use HadCRUT4 global mean temperature data, available as annual data here. The difference between the mean for the decade 2002–2011 and that for 1871–1880 is 0.727°C. The uncertainty in that temperature change is tricky to work out because the various error sources are differently correlated in time. Adding the relevant years' total uncertainty estimates for the HadCRUT4 21-year smoothed decadal data (estimated 5–95% ranges 0.17°C and 0.126°C), and very generously assuming the variance uncertainty scales inversely with the number of years averaged, gives an error standard deviation for the change in decadal temperature of 0.08°C (all uncertainty errors are assumed to be normally distributed, and independent except where otherwise stated). There is also uncertainty arising from random fluctuations in the internal state of the climate. Surface temperature simulations from a GCM control run suggest that error source could add a further error standard deviation of 0.08°C for both decades. However, the matching of their characteristics as set out in the main text, points a) to c), and the fact that some fluctuations will be reflected in OHU, suggests a reduction from the 0.11°C error standard deviation implied by adding two 0.08°C standard deviations in quadrature, say increasing halfway, to 0.095°C. Adding that to the observational error standard deviation of 0.08°C gives a total standard deviation of 0.124°C.
The change between 1871‑1880 and 2002–2011 in decadal mean AF, with aerosol forcing scaled to reflect the best recent observational estimates, is 2.09 W/m², taking the average of the Figure 8.18 and RCP4.5 derived estimates (which are both within about 1% of this figure). The total AF uncertainty estimate of ± 0.87 W/m² in Table 8.7 equates to an error standard deviation of 0.44 W/m², which is taken as applying for 2002–2011. Using the observational aerosol forcing error estimate given in Section 7.5.3 instead of the corresponding Table 8.7 uncertainty range gives the same result. Although there would be some uncertainty in the small 1871–1880 mean forcing estimate, the error therein will be strongly correlated with that for 2002–2011. That is because much of the uncertainty relates to the relationships between:
- concentrations of WMGG and the resulting forcing
- emissions of aerosols and the resulting forcing,
the respective fractional errors in which are common to both periods. Therefore, the error standard deviation for the change in forcing between 1871–1880 and 2002–2011 could well be smaller than that for the forcing in 2002–2011. However, for simplicity, I assume that it is the same. Finally, I add an error standard deviation of 0.05 W/m² for uncertainty in volcanic forcing in 1871–1880 and a further 0.05 W/m² for uncertainty therein in 2002–2011, small though volcanic forcing was in both decades. Solar forcing uncertainty is included in Table 8.7. Summing the uncertainties, the total AF change error standard deviation is 0.45 W/m².
I estimate 2002–2011 OHU from a regression over 2002–2011 of 0–2000 m pentadal ocean heat content estimates per Levitus et al. (2012), inversely weighting observations by their variance. OHU in the 2000–3000 m layer is estimated to be negligible. After conversion from zeta Joules/year, the trend equates to 0.433 W/m², averaged over the Earth's surface. The standard deviation of the OHU estimate as computed from the regression residuals is 0.031 W/m², but because of the autocorrelation implicit in using overlapping pentadal averages the true figure will be much higher. Multiplying the standard deviation by sqrt(5) provides a crude adjustment for the autocorrelation, bringing the standard deviation to 0.068 W/m². There is no alternative to using GCM-derived estimates of OHU for the 1871–1880 period, since there were no measurements then. I adopt the OHU estimate given in Gregory 02 for the bracketing 1861–1900 period of 0.16 W/m², but deduct only 50% of it to compensate for the Levitus et al. (2012) regression trend implying a somewhat lower 2002-2011 OHU than is given in the SOD. Further, to be conservative, I treble Gregory 02's optimistic-looking standard deviation, to 0.03 W/m². That implies a change in OHU of 0.353 W/m², with a standard deviation of 0.075 W/m², adding the uncertainty variances. Although Gregory 02 ignored non-ocean heat uptake, some allowance should be made for that and also for any increase in ocean heat content below 3000 m. The (slightly garbled) information in Section 3.2.5 of the SOD implies that 0–3000 m ocean warming accounts for 80–85% of the Earth's total heat uptake, with the error standard deviation for the remainder of the order of 0.03 W/m². Allowing for all components of the Earth's heat uptake implies an estimated change in total heat uptake of 0.43 W/m² with an error standard deviation of 0.08 W/ m². Natural variability in decadal OHU should be the counterpart of natural variability in decadal global surface temperature, so is not accounted for separately.
Appendix 3: Derivation of the 5–95% confidence interval
In the table of changes in the variables between 1871–1880 and 2002–2011, I split the AF error standard deviation between that for CO2 and other greenhouse gases (0.291 W/m²), and for all other items (0.343 W/m²). The reason for doing so is this. Almost all the SOD's 10.2% error standard deviation for greenhouse gas AF relates to the AF magnitude that a given change in the greenhouse gas concentration produces, not to uncertainty as to the change in concentration. When estimating ECS, whatever that error is, it will affect equally the 3.71 W/m² estimated forcing from a doubling of equivalent CO2 concentration used to compute the ECS estimate. Most of the uncertainty in the ratio of AF to concentration is probably common to all greenhouse gases. Insofar as it is not, and the relationship between changes in greenhouse gases is different in the future to in the past, then the two AF estimation fractional errors will differ. I ignore that here. As most of the past greenhouse gas forcing is due to CO2 and that is expected to be the case in future, any inaccuracy from doing so should be minor.
So, I estimate a 5–95% confidence interval for ECS as follows. Randomly draw a million realisations from each of the following independent Normal(mean, standard deviation) distributions:
a: AF WMGG uncertainty – before scaling – from N(0,1)
b: Total AF without WMGG uncertainty – from N(2.09,0.343)
c: Earth's heat uptake – from N(0.43,0.08)
d: Surface temperature – from N(0.727,0.124)
and for each quartet of random numbers compute ECS as: 3.71 * (1 + 0.102*a) * d / (0.291*a + b − c).
One then computes a histogram for the million ECS estimates and finds the points below which 5% and 95% of the total estimates lie. The resulting 5–95% range comes out at 1.03 to 2.83°C.
 Bishop Hill
Bishop Hill
Judith Curry's reaction is here.
Nic Lewis in the post at BishopHill does a very nice empirically based sensitivity analysis following the general methodology of the Gregory et al (2002) heat balance change derived value of the equilibrium climate sensitivity, determining a value of ECS of 1.6-1.7C. While there are some necessary assumptions in empirically based sensitivity analyses that I am not entirely comfortable with, the qualitative conclusion made by Nic Lewis seems robust: lower values of ECS seem justified in view the reduce values of aci.


Reader Comments (64)
Just to remind readers comments will be tightly moderated for tone and relevance.
And just to say thank you to Nic and the Bish for making BH 'home' for these crucial findings.
Thanks for posting the calculations, Nic.
Beyond my poor scientific comprehension, but thanks to Nick (and of course many others) for fighting the good fight on behalf of the integrity of science.
Would appreciate a pointer to a brief bio for Nic Lewis.
Nice bed time reading for Brian C. and Robin I. No doubt they will comment here tomorrow. I won't be expecting a damascene conversion.
Looking forward to studying this post. Thank you very much for putting it here.
The term 'forcings' seems to have been introduced fairly recently - 1980s? - and I am keen to see how it is being used and explained. The GCM usage, which is where I think it started, seems clear - it is the value of a step change in outgoing radiation to be imposed at the top of model atmospheres as a deliberate kick to the system. As the system responds by re-adjusting to the kick (e.g. generally to warm up if the kick called for a reduction in outgoing radiation as per CO2 or such like, or to cool down if the reduction was negative, i.e. an increase, in the case of aerosols for example). In practice, a collection of these 'forcings' is compiled, and their overall net 'forcing' is then applied - at least in the simplest model run experiments.
Now the radiation imbalance at the top of the real atmosphere is not really a driver of anything, so much as a consequence of what is going on below and coming in from above, and of course there are other problems with the method which are well known (e.g. can all the forcings be just added up to find a net one, do some of them interact, are some of them heterogeneuous in space). But the method of 'forcings' clearly has great appeal from a computational viewpoint, allowing the same mechanism to be used to incorporate the presumed effects of many different factors in a very simple way.
The real climate system is of course dominated (driven) in the troposphere by heat transfers from the surface upwards. These are the genuine 'forcings' in my book, and will be influenced by cloud cover, aerosols, surface conditions, and atmospheric and ocean states and movements. So the negative 'forcing' associated with aerosols for example, is presumably linked to their reducing insolation reaching the surface during the day, and in that sense has a physical meaning.
I hope no one minds my taking up space here with these ramblings - they are relevant to the topic, but are a bit of a shirt-trailing exercise to draw fire and corrections to my very unsure grasp of what has been going on in this area. From a skim through of the above post, I think it promises to help me get a far better idea of the heat balance method is used along with notional 'forcings' to get an estimate of climate sensitivity that is not reliant on GCMs. Perhaps others are also looking to personally benefit from using this to improve their understanding? Let others grapple with the odious IPCC, I just want to be able to think more clearly!!
Wow is this how science is supposed work, observation then rework theory rather than massage and cherry pick data.....
John Shade
May I suggest that you read section 8.1 of the leaked AR5 WG1 SOD for an explanation of how the term forcings - both radiative and adjusted - is used? Available at http://www.stopgreensuicide.com/Ch8_Radiative-forcing_WG1AR5_SOD_Ch08_All_Final.pdf
Thanks. Will do.
[Snip. Not on this thread please]
Does this assume that the earth and particularly the ocean is in equilibrium now? At first look I would think this is more like an estimate of transient climate sensitivity (and it happens to be close to the IPCC number for TCS). If not then what number does this approach give for TCS?
This relates to a larger problem that I have with the idea of cleanly separating out 'observational' from 'model based' estimates, which I don't think can really be done. We have no direct observations of equilibrium climate sensitivity so we have to rely on some form of theory or indirect observations from paleo, at least in part.
But a short answer to my question about whether this estimate assumes equilibrium would be great.
The Gregory et al. (2002) paper on estimating climate sensitivity using a simple observationally based heat balance approach is available here (not paywalled): http://journals.ametsoc.org/doi/pdf/10.1175/1520-0442%282002%29015%3C3117%3AAOBEOT%3E2.0.CO%3B2
Gregory 02 provides a good explanation for the basis of what I have done, although its observational data (and its model derived aerosol forcing change) has now been superceded.
Nic,
Have you seen "Satellite methods underestimate indirect climate forcing by aerosols" published in PNAS by Penner et al.? This is something you may want to address if/when you write up for review.
Biosketch. Nic Lewis’ academic background is mathematics, with a minor in physics, at Cambridge University (UK). His career has been outside academia. Two or three years ago, he returned to his original scientific and mathematical interests and, being interested in the controversy surrounding AGW, started to learn about climate science. He is co-author of the paper that rebutted Steig et al. Antarctic temperature reconstruction (Ryan O’Donnell, Nicholas Lewis, Steve McIntyre and Jeff Condon, 2011, Improved methods for PCA-based reconstructions: case study using the Steig et al. (2009) Antarctic temperature reconstruction, Journal of Climate – print version at J.Climate or preprint here).
(from JC)
JK
No, my method - which follows the estimation of climate sensitivity in Gregory 02 - does not assume that the ocean is in equilibrium now. Hence the deduction of the estimated change in ocean heat uptake from the estimated change in forcing before comparison with the change in global temperature to derive sensitivity.
Transient climate sensitivity (or more commonly Transient climate response - TCR) is the change in global temperature after a 70 year period in which forcing, increasing linearly, rises by 3.71 W/m^2 - that is, what forcing a doubling of CO2 concentration produces. It is in my view an artificial parameter, which conflates equilibrium climate sensitivity and ocean heat uptake parameters (mixed layer depth, effective vertical diffusivity, upwelling strength). Moreover, TCR is only valid over a 70 year period. (Myles Allen takes a different view on the relative merits of ECS and TCR.)
Since the heat balance approach does not involve estimating ocean parameters, it does not provide an estimate of TCR. But a quick computation suggests that with ECS at 1.6 C and reasonably mainstream ocean heat uptake parameters, TCR would likely be in the range 1.25 -1.4C.
Nic
An interesting point over at WUPT:
"If there is “warming in the pipeline”, this analysis will underestimate ECS."
How would you respond to that?
[Let's do that on another thread]
This maybe better off being (cross) posted over at Climate Audit, it'll get a more technical appraisal, IMHO.
AndyL
Re point raised at WUWT: "If there is “warming in the pipeline”, this analysis will underestimate ECS."
I have responded there but my comment hasn't as yet appeared.
The point is wrong. Warming in the pipeline very largely reflects ocean heat uptake, which reduces the extent to which surface temperatures need to rise in order to counteract increased forcing from CO2 etc. My analysis adjusts for ocean heat uptake.
The Gregory et al. (2002) study - which uses essentially the same method - explains this point in more detail. It is available here (not paywalled).
Thanks, much clearer after looking at Gregory 02.
If I understand correctly your estimate and error for ocean heat uptake are for average rate over the period 1880-2011, while your estimate of the forcing rate and associated delta T are for 2011.
Have you considered the possibility of century scale acceleration in OHU? If, for the sake of argument OHU in 2011 were twice that of the 1880-2011 average then the ECS estimate rises to 2.2 degC. That's still below 3 degC, but does demonstrate some sensitivity of the estimate to this factor.
The IPCC's response, I think, will be to maintain that the Earth's Heat Uptake, in the sense of warming oceans, is much greater than previously thought. This from Chapter 3 Page 10 Lines 23-28
The SPM admits AR4 overstated aerosols. AR5 has detected the missing heat in the deep oceans below 3000m. This is based on sparse sampling.
JK
"If I understand correctly your estimate and error for ocean heat uptake are for average rate over the period 1880-2011, while your estimate of the forcing rate and associated delta T are for 2011."
No, for each of ocean heat uptake (OHU), forcing and temperature I compute the change therein between the average over 1871-1880 and the average over 2002-2011. OHU for 2002-2011 is estimated by regressing the change in ocean heat content over that period against time. OHU for 1871-1880 is based on the AOGCM-simulation derived estimate for 1861-1900 given in Gregory 02 (just above the Results section). See the last section of my Appendix 2.
ManicBeancounter
"AR5 has detected the missing heat in the deep oceans below 3000m. This is based on sparse sampling."
Yes, but the "missing heat" is not very large and I think there may anyway be an element of double counting here. My estimate of climate sensitivity does actually allow for ocean heat uptake (OHU) below 3000m. See the reference in the last section of Appendix 2 to that effect. I increased my calculated change in OHU to allow for sub-3000m OHU and for heat uptake by other components of the climate system.
Andrew can you point us to a bio for Nic, is he a close shaved or a facial hairy "climatologist"
Even using a GCM to calculate the thermal inertia due to heat uptake by Oceans and assuming that all the observed temperature rise since 1850 is caused only by enhanced CO2 still only results in a climate sensitivity of 2 deg ! Thermal inertia and climate feedbacks.
Most likely the sensitivity is 1.5 C , since a natural 60 year oscillation is evident in the temperature data. Temperature should then peak around 2280 at 2 degrees above natural levels before returning to a natural norm by year 3000-4000 AD.
In short : No big problem !
"AR5 has detected the missing heat in the deep oceans below 3000m."
This begs the question: "If the worlds accumulated heat can be so quickly transported down to below 3000m in the Southern Oceans then why doesn't it also take carbon dioxide with it?"
Diffusion is not fast enough for either, so mass transport is being invoked.
I have a post on this at
http://judithcurry.com/2012/12/19/climate-sensitivity-in-the-ar5-sod/
Thank you Nic. Nice to see the detail and follow the rational reasoning.
In the meantime, back in cotton wool land:
"Since the time of AR4, neither global mean temperature nor OHU have increased, while the IPCC's own estimate of the post-1750 change in forcing net of OHU has increased by over 60%."
The key seems to be the summary at JC - this needs wider circulation IMHO - maybe the report will be more realistic then (ok, I hope it will be) :
JC summary: The leak of the SOD was a good thing; the IPCC still has the opportunity to do a much better job, and the wider discussion in the blogosphere and even the mainstream media places pressure on the IPCC authors to consider these issues; they can’t sweep them under the rug as in previous reports.
michael hart
"Diffusion is not fast enough for either, so mass transport is being invoked."
You are quite right. In fact, pure diffusion is too slow even way above 3000 m, particularly as it has to fight against upwelling. The transport process can be approximated by an equivalent diffusion process but, as I understand it, actually relies much more on isopycnal transport (along sloping surfaces of constant density), etc. But the warming below 3000 m is linked to water sinking from the surface to form bottom water, principally close to Antarctica. See the Pukey and Johnson paper: http://www.pmel.noaa.gov/people/gjohnson/gcj_3w.pdf . Whether it is right I couldn't say.
Surely the descending water does take CO2 with it?
@ morph re: The JC Summary
Someday, I'll get to tell the backstory of all this.
Nic Lewis
Thanks for your very interesting post, likely to push out my proposed reading. Also many thanks for the link to Purkey and Johnson paper.
Whilst I know this is very simplistic, but am I to assume that the driver behind the Purkey and Johnson is not that they found increased temperatures in the ocean depths but that the percieved TOA imbalance sent them looking for where it might be?
Bish: "This is a guest post by Nic Lewis. Please note that comments will be tightly moderated for tone and relevance."
I see that whilst you seem to be adopting a very heavy-handed approach towards censoring the comments of regular registered posters on this site, you still haven't banned the cornish cockroach, despite its continued offensive, abusive and threatening remarks to other posters. Why?
[BH adds: You mean Zed? There are limits to what I can do to ban people. IP blocks are only semi-effective]
Nic,
Many thanks for your response on the deep heat in the oceans. I should have read the source of the deep heat claims (Kouketsu et al., 2011) more closely. I was misled by
1. The abstract of Kouketsu et al. claiming "large temperature increases were detected around Antarctica" for the period 1990s to 2000s, with impressive red areas on Figure 3. The highest warming rates were 0.01°C per decade or less.
2. The prominence given in the SPM to the Southern Oceans warming. It must be a big issue to gain such prominence.
3. The quoting of the equivalent energy (large units), rather than the actual impact. In a similar way I was alarmed by the notion that the ice caps were losing by hundreds of gigatonnes of ice (1Gt = 1km3 water) per year, until I calculated the sea level rise equivalent in mm.
Having re-read you article, you appear to relate one element to another quite tightly, along with stating your assumptions. I would be surprised if any critical response would be to this standard.
Hi Nic
Thanks for a very interesting post.
One key point is whether the simple method you've used here provides a reliable estimate of ECS, which is defined as the long-term change in global mean temperature for a doubling of the CO2 concentration, once the temperature has reached equilibrium. The reason that models are used to estimate this is because this in itself cannot be measured using the instrumental record, as we've not yet seen a doubling of CO2. To use the instrumental record directly, it is therefore necessary to make some assumptions. You've used a common approach where the observed temperature change takes the place of the equilibrium temperature change term, and the observed RF takes the place of the RF for doubled CO2 - and knowing the RF for doubled CO2, it's just a matter of using the ratios as you do in your paragraph starting "Now comes the fun bit". Of course that by itself wouldn't work as the temperature hasn't had time to reach equilibrium, so this is usually accounted for by subtracting the ocean heat uptake from the RF (and again, you did do that - you are essentially following the recipe of Rahmstorf 2008 but with updated numbers).
The question is, does this really properly represent what the response to a doubling of CO2 would be, taking into account all the complexities of the climate system and the uncertainties in the other forcings. There's quite a few things to consider which make it more complicated (one which particularly interests me is the RF due to land cover change and also other non-radiative effects of land cover change on temperature). Judith Curry also mentions assumptions that she's "not entirely comfortable with", and she ends up hedging her bets and saying that your qualititative conclusion seems robust, that lower ECS seems justified by the smaller -ve aerosol forcing. This seems fair enough to me - but the million dollar question is, how much lower is it? While ideally it would be good to use a purely observationally-based estimate, I'm not yet convinced that we can iron out the assumptions enough to give a really good estimate, and hence (in my view anyway) there is still a need to use models which give a more complete picture of the complexities of the climate system. I realise that this will be a contentious thing to say here :-) In practice, the best thing is to try to use the models and observationally-based estimates (remembering their assumptions) together to see where we are getting a consistent picture and where there are inconsistencies between the approaches, to try to actually understand how the details of the climate system really work.
Incidentally, I'd still hold out hope for palaeo estimates of ECS also being a useful addition to the mix. I'm sure we're all looking forward to Tamsin's results that she teased the RMS meeting about the other week... :-)
But thanks again Nic for an interesting and constructive contribution to the discussion on this extremely important topic. It will indeed be interesting to see what the final assessment of ECS looks like in AR5 WG1 (the SOD is of course still only a draft, the chapters could still change in the light of review comments)
Did Nic submit this as an Ar5 SOD review comment subject to the confidentiality agreement, or has he sidestepped the process?
Richard Betts,
I agree with you that observations may not capture the complexities. But doesn't it come down to the presumption that feedbacks are linear? We hope that changes are small enough that this will be true, and this seems plausible, although not proven, for important feedback such as water vapor and clouds. I'm not sure if you think your land cover feedbacks should be strongly non-linear.
But if we think that non-linear effects are so important then doesn't the concept of climate sensitivity go out of the window anyway? Of course that doesn't mean that feedbacks have to be linear (or that Nic Lewis has done his analysis correctly). But to the extent that climate sensitivity is a useful concept, shouldn't this methodology get at it?
Richard Betts -
You write: "There's quite a few things to consider which make it more complicated (one which particularly interests me is the RF due to land cover change and also other non-radiative effects of land cover change on temperature)."
Could you please clarify the issue of "RF due to land cover change." That is, my understanding is that there is an RF attributed to LU/LC, and presumably Nic has included it in his calculations above. Is it that you don't believe that the RF (or AF) is well estimated? Or that the error bars on this figure are inapt?
With regard to LC effect on surface temperature, I would think that to the extent that there's any validity in the "climate sensitivity" approach -- that is to say, that a change in average surface temperature can be said to cause a proportional increase in radiated energy at TOA -- it should be possible to adjust the standard formula to allow for such an effect. I'm presuming that you're positing a LC effect on average surface temperature which doesn't affect the emitted thermal radiation, or something like that. What are the reasonable limits to such an effect which would be observable to date? [Or perhaps again I'm not quite following.]
Thanks in advance.
Hi Richard
You are right that surface processes affect carbon balance and therefore climate. But (a) projections of alarm were made by the IPCC in early 1990, and the environmental conferences even much earlier when such processes were barely incorporated into climate models. The defense of such projections is being pursued even today, witness articles in any given Nature issue. (b) Look at the latest Science issue. There is a small news item about giant viruses infecting zooplankton which affects ocean carbon flows. Surely there is not a single virus in any GCM, let alone whole ecosystems of them. Any unknown unknown will only eat away from the attributional strength and proportion currently endowed upon CO2. Under these circumstances, it is not necessarily clear that more modelling with bring any greater clarity.
Nic,
An excellent study. I have performed a similar one, unsing somewhat different assumptions, but arriving at a very similar answer. I did not use observational aerosol forcing estimates, but instead made use of the fact that anthropogenic aerosol forcing is much greater in the Northern Hemisphere than in the Southern hemisphere. Put in a two-hemisphere energy-balance model and using observed hemispheric temperature changes and ocean heat uptake changes you can easily arrive at an independent total aerosol forcing estimate - one that also implies small net total aerosol forcings that are reasonably consistent with the latest observatiional findings. My nominal ECS range is very close to yours, though slightly smaller and with similar uncertainty bounds. The chance that the ECS is less that 2 degrees C is, in my opinion, 80% or greater and high ECS values are, in effect, ruled out.
I might also note that the method returns ECS values that are generally similar to those reported for AR5 GCMs when ECM-derived temperature and ocean-heat-uptake predictions are input to the model instead of the observed values (AR5 GCM values are obtained from the "Climate Explorer" web site). The GCMs appear to be wrong not only because they assume too much aerosol cooling, but also because, a) most of them arrive at a too-high temperature change between the 1880-1890 and 2000-2010 time frames, and b) because they generally predict too much ocean heat uptake, particularly in the Southern Hemisphere. The high Southern Hemisphere ocean heat uptake compensates for the too-high aerosol cooling in the Northern Hemisphere to allow the GCMs to get relative hemispheric temperature changes that are more-or-less in the right ballpark, but for the wrong reason. Because of the too-high sensitivity they also over-predict volcanic cooling effects, but the AR5 assumed forcings minimize that problem by halving volcanic aerosol forcing over previously used (and in the case of Pinatubo, observed) values.
One other major problem with the AR5 report is that that the "scary" rcp 8.5 secnario burns far more fossil fuel than appears to be geologically available. Even allowing for generous new discoveries it is unlikely that the CO2 concentrations will ever get much over 600 ppmv. These factors all combine to imply that green-house-gas induced temperature changes can never exceed a degree or two over present values, and will almost certainly begin to decrease in the 22nd century no matter what draconian "carbon-control" policies are or are-not instituted today. The fact that such limits are not even addressed in the AR5 report is revealing.
[O/T]
So much is based on temperature measurements, which still have great uncertainty. For example, using 1880-90 as a reference period invokes the bucket problem for surface sea temperatures. How does one account uncertainty in past adjustments when these are absolute changes of bias, often little more than a guess, and not statistical ranges amenable to precision-style statistics? Do we accept the error estimates in HadCRUT4? Many do not.
Temperature uncertainty must play a large part in the puzzles of Chap 3 Oceans fig 3.3a, where the Southern ocean temperatures perform rather differently to the Northern. At page 3.44 we read "It will take centuries to millennia for deep ocean temperatures to warm in response to today’s surface conditions." Sadly, these deep southern waters are said come from parts of the globe with extremely sparse temperature sampling. Yet graph 3.3a shows warming today, giving yet another example of many of the confused relationships between static and dynamic events or assumed events. Factors like lags and accumulation deserve further study (e.g. Stockwell).
(It is surprising how many global events become recognised in the prime publishing eras of authors, another dynamic event).
But this is a game-changing essay and I can only concur, after giving a couple of uncertainties, with Judith Currie's reservations about empiricism.
The estimated sensitivity was first reported as 3C +/-1.5C in the Charney Report 1979, it was changed for no apparent reason to 3C +1.5/-1C in AR4. 33 years on we haven't moved forward from Charney's educated guess. What's going on?
[snip. DNFTT}
The models are adequately debunked by Gerry Browning in an old post at Climate Audit. I know Gerry and he should be taken seriously, his arguments are rigorous and serious. I also have held forth on this subject. Basically, there is no scientific reason to accept the accuracy of GCM's for climate. The numerical methods are old and in some cases very poor, the subgrid models are dubious and even much simpler fluid dynamical systems cannot be accurately be predicted even using more modern numerical methods. Basically, the initial value problem for the Navier-Stokes equations is ill-posed, a fact that has been well known for 50 years.
I think Richard (Betts) gave quite a good assessment.
I think the post (here) and it's connections to the Matt Ridley's column have more than one dimension.
First the technical one. Assuming (cause I wasn't so thorough as to redo them) that Nic Lewis calculations are correct and noting that I do however wonder whether all uncertainties are considered, there is a weakness in terminology on the science-side. Not from Nic Lewis but from the published science. What Gregory calls ECS is not equivalent to the ECS from the model-studies. We would expect the Gregory-ECS to be closer to the Transient Climate Response estimates since it is not calculated from equilibrium assumptions, and indeed it is closer to TCR. I think Gregory (and also the Third AR) called it effective CS. That is Nic Lewis estimate doesn't contradict or invalidate nor is it incompatible with the simulation-based estimates.
However, and that's the second dimension of the post, there's a question in the title. The simple answer may be the IPCC-procedures concerning peer-review, which is an unsatisfactory and lazy reply. As far as I see the AR5SOD doesn't consider the Gregory approach. Which is another unsatisfactory answer. So, I would expect that the writing team would be interested to include an updated instrumental estimate based on the newest forcing estimates. However, there are some quite low estimates in the respective AR5Figures anyway.
One more note. I wrote yesterday on twitter that Aldrin does not give the most likely as 1.6C. I guessed 1.9C (although I rather read it as 2C). Gavin (Schmidt) notes in my feed: "Fig 6a has 5-95% as 1.1-4.3C, mean=2C. ...".
The Aldrin data is considered in the AR5draft.
With respect to the Ring et al. result I think, but I'm not sure, that the caveats re:equilibrium apply as well.
Like Richard I do think we need the Paleo-estimates (due to the evasiveness of (E)CS).
I guess many would appreciate it if Lewis would submit his analysis (analyses) to a journal. As noted at another location, it would be best for people doubting the peer-review-system to submit to an EGU-open-access-open-review-journal. However, there's the question of the author-charges. PlosONE generally is apparently good at waiving such charges. Lewis work may fit well in Atmospheric Science Letters (http://onlinelibrary.wiley.com/journal/10.1002/%28ISSN%291530-261X/homepage/ForAuthors.html) which however is paywalled and blind-reviewed.
Some fun-reading on model-related CS is the PhD-thesis of D. Klocke ("Assessing the uncertainty
in climate sensitivity", just google it)
The question on GCMs is, what is the accuracy of this statement?
"None of the models used by IPCC are initialized to the observed state and none of the climate states in the models correspond even remotely to the current observed climate. In particular, the state of the oceans, sea ice, and soil moisture has no relationship to the observed state at any recent time in any of the IPCC models. There is neither an El Niño sequence nor any Pacific Decadal Oscillation that replicates the recent past; yet these are critical modes of variability that affect Pacific rim countries and beyond. The Atlantic Multidecadal Oscillation, that may depend on the thermohaline circulation and thus ocean currents in the Atlantic, is not set up to match today’s state, but it is a critical component of the Atlantic hurricanes and it undoubtedly affects forecasts for the next decade from Brazil to Europe. Moreover, the starting climate state in several of the models may depart significantly from the real climate owing to model errors. I postulate that regional climate change is impossible to deal with properly unless the models are initialized."
Kevin Trenberth 4th June 2007
If I may include something slightly less serious, Bishop...simply splendid headline on NoTricksZone:
IPPC5 AR now claims anthropogenic warming is offset by anthropogenic cooling.
http://notrickszone.com/2012/12/19/ ipcc-5-ar-now-claims-anthropogenic-warming-is-offset-by-anthropogenic-cooling-youve-got-to-be-kidding/
Made my day!
@Richard Betts.
Some observations. Any one of which completely undermine catastrophic AGW theory.
Can we believe the observational data? Probably not as it is been fiddled to fit with models.
http://hockeyschtick.blogspot.co.uk/2012/12/massive-data-manipulation-at-nasa-warms.html
NO trend in global water vapour- a bit of a problem for the "positive feedback" found in GCMs.
http://www.forrestmims.org/
Not surprisingly temperatures are not responding as the IPCC predicted (or hoped?).
http://wattsupwiththat.com/2012/12/14/the-real-ipcc-ar5-draft-bombshell-plus-a-poll/
Finally it looks like the Sun has more influence (now there's a shock) on climate than supposed.
Solar Irradiance Modulation of Equator-to-Pole (Arctic) Temperature Gradients: Empirical Evidence for Climate Variation on Multi-decadal Timescales
http://www.sciencedirect.com/science/article/pii/S136468261200288X
All in all some worrying data for those who rely on CAGW for their pay cheques.