 Bishop Hill
Bishop Hill Koutsoyiannis 2011
 Jun 6, 2011
Jun 6, 2011  Climate: Surface
Climate: Surface This is a guest post by Doug Keenan.
Two months ago, I published an op-ed piece in The Wall Street Journal. The piece discussed the record of global temperatures, illustrated in the figure.
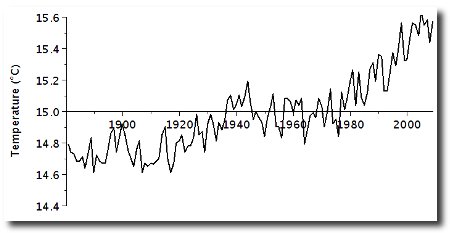
The IPCC, and most climate scientists, have claimed that the figure shows a significant increase in temperatures. In order to do so, they make an assumption, known as the “AR1” assumption (from the statistical concept of “first-order autoregression”). The assumption, however, is simply made by proclamation. The failure of the IPCC to present any evidence or logic to support its assumption is a serious violation of basic scientific principles. Moreover, it turns out that the assumption is insupportable: i.e. there is conclusive evidence that the assumption should not be used. (Further details are given in the op-ed piece; what follows assumes background given there.)
Without making some statistical assumption, we cannot analyze the global temperatures. Hence we cannot determine whether temperatures have been significantly increasing. The crucial question, then, is this: what assumption should be used in analyzing the global temperatures?
A research paper that appears to make major progress in finding an answer to that question was published on April 15th. The paper is
Koutsoyiannis D. (2011),
“Hurst–Kolmogorov dynamics as a result of extremal entropy production”,
Physica A, 390: 1424–1432.
doi:10.1016/j.physa.2010.12.035
Following is a partial summary of what the paper indicates for the global temperature series.
Consider this statement: “The temperature of Earth this year affects the temperature of Earth the next year; for example, if this year is cold, then the next year will probably be colder than average”. That statement is accepted by virtually all climatologists, and it is accepted in the most-recent report from the IPCC (§I.3.A).
Koutsoyiannis (2011) assumes that the above statement can be generalized by replacing “year” with any other time span, e.g. “day”, “minute”, “millennium”. He also assumes that the climate system adheres to the second law of thermodynamics (thus entropy is always maximized). From those assumptions, he calculates the approximate formula that the time series for temperatures must have.
The formula has been known for a long time. It is usually called “stochastic self-similar scaling”, although here Koutsoyiannis calls it “Hurst-Kolmogorov”. It has been known for decades that many climatic processes seem to conform to the formula. Yet the formula has not been accepted for such processes, because there seemed to be a problem with it: it seemed to require e.g. that the temperature from some year a century ago affected the temperature this year—and that is not physically plausible. Koutsoyiannis resolves the problem. The temperature from some year a century ago does not have a significant effect on the temperature this year. Rather, the temperature from the last century has a significant effect on the temperature this century, etc.
Koutsoyiannis' paper actually deals with any system for which his assumptions are reasonable. The paper does not analyze the global temperature series, but previous work of Koutsoyiannis does and shows that the formula fits the series well. If the formula is valid for the series, then the conclusion is that there has not been a significant increase in global temperatures. That is, the changes that appear in the figure above can be reasonably ascribed to chance fluctuations.
That does not mean that carbon emissions have not caused an increase in temperatures. As an illustration, suppose that we have a coin and we want to determine whether the coin is biased. We toss the coin three times, and it comes up Heads, Heads, Heads. Getting three Heads out of three tosses might well occur by chance, or it might be due to the coin being biased. That is, we cannot really conclude anything. Similarly with the global temperature series: under the assumptions of Koutsoyiannis, the series is far too short to conclude anything.
As noted, Koutsoyiannis' paper applies to a wide variety of natural systems. Hence the foregoing applies not just to global temperatures, but also to many more time series. In other words, it is unlikely that we will be able to find any empirical evidence for significant global warming. The case for global warming therefore rests almost entirely on computer simulations of the climate.


Reader Comments (42)
"The case for global warming therefore rests almost entirely on computer simulations of the climate."
Amazing, that graph, the rise in temps, if the graph can be believed [?] seems to coincide with a man made conjecture [AGW] and just when the temperature record [hundreds of weather stations disappeared] was rigged by Hansen's GISS - coincidence?
No s**7.
Mention of second law and lapse rates seals the argument, AGW can only be realised by computer generated 'hot spots' in the ITCZ - which controverts second law of thermodynamics.
End of hypothesis.
Unfortunately our Hyperthermalist chums don't do logic.
Or thermodynamics.
Or science.
Or statistics.
Or honesty.
Re Athelstan,
When you examine (say) the hot year 1998, you find that it is hot because there are a few stations - more than in a usual year - showing it is quite hot, while the rest carry on as normal. It is NOT because all stations uniformly show a hot year, so that their linear combination is hot. I can show you stations where 1998 was colder than surrounding years.
Under these circumstances, there are several possibilities. One is that we are dealing with noisy data, so that a year that WAS hot showed cold because of errors, or vice versa. Another is that there is a global effect operating in a spotty way, where some stations are affected by a global influence, but others are not. This type of explanation can be supported by stations that seem out of line not over just a hot year, but over many decades. The Antarctic stations of Australia and nearby Macquarie Island show essentially no warming in the last 40 years, for example. The consequence is that CO2, if it is the culprit, is somehow selective, affecting some places for 40 years, but not others.
Another possibility is related to your comment about the reduction in the number of reporting stations.
Where the data are noisy, or where the effect is selective at the hand of man, YES, the system can be cherry picked to show a desired outcome.
Please, take care with statements on the Second Law of Thermodynamics. It is often misunderstood.
It seems entirely reasonable that tomorrow's temperature is affected by today's or that this year's temperature is affected by last year's. This can be explained by energy in the system which persists from day to day or year to year. It seems a lot less reasonable to assume one century's temperature is affected by the previous century's. What is the mechanism for this?
'Koutsoyiannis (2011) assumes that the above statement can be generalized by replacing “year” with any other time span, e.g. “day”, “minute”, “millennium”'
This does not seem a valid assumption without an explanation.
Julian
It seems reasonable to me on its own terms.
If one accepts that this year's temperature is much like last year's, which the writer is saying most psyentists do, then there is logically not a lot of difference between that and a similar proposition made with the time interval changed.
In the same way that a coin doesn't know about probability but still comes down heads around half the time, likewise, the climate doesn't need to "know" what year, decade or century it is to repeat the previous one.
No?
Doug
I agree with the first part, that one needs to make an assumption about the underlying statistical properties of a (i.e. the climate-) system, to at all make any tangible sense when characterizing it.
But isn't the assumption that the climate has selfsimilar scaling properties also just another ad hoc asumption? Albeit a more reasonable one than a linear underlying trend?
Re: Julian,
From Koutsoyiannis assumptions he generates a “stochastic self-similar scaling” formulae. This is then applied to the temperature series to see how it fits. Because it fits quite well it indicates that his assumptions are valid.
The only evidence to support the “first-order autoregression” assumption (and hence significant warming) is the output from computer models.
Unlike the computer models, Koutsoyiannis assumptions can be applied to the entire ice core record to see how it performs. Since the article already mentions millennium time scales I assume it already has been tested.
The coin example is interesting. Suppose I weight a coin to bias it to show heads. To test my handiwork I try three tosses and they come up Heads. I conclude that I have done well: my experiment confirms the hypothesis that the coin is biased.
The analogy for global warming is that there is a physical theory that adding CO2 to the atmosphere will result in higher temperatures. We check the (recent) temperature record - temperature is rising (suppose). The temperature series confirms the hypothesis that the temperature is rising.
Returning to the coin ... suppose there are two coins A1 and A2 in an urn. Coin A1 is biased and the probability of getting heads when you toss it is 0.75. Coin A2 is fair, the probability of heads is 0.5. I draw (without looking) one of the coins from the urn and toss it three times. It shows three heads. What is the probability that it was the biased coin I picked? This is an exercise in Bayes Theorem (see Wikipedia). Assuming that the "prior" probability of picking the biased coin was 0.5 then the so-called "posterior" probability that I picked the biased coin given I got three heads is in fact 0.77. The experiment confirms the hypothesis
I don't have the knowledge/skill to see if Bayesian style reasoning applies to time series of temperature. But allowing that the (recent) record is not long enough to be statistically significant does that mean that it is entirely irrelevant to the question of global warming?
A fascinating post - many thanks.
Justice4Rinka:
I hope very much this was not a typo, but instead the very clever mash-up I take it for?
...saying most psyentists do...
I'm prepared to accept that Koutsoyiannis has found that his theory fits the temperature record (TerryS) but only as a starting point. I still want to know what the mechanism is. I can imagine a mechanism that means one cold year influences the next one to be cold. i.e. It takes longer than a year for the sun to provide enough energy to warm the earth up. That seems reasonable. I cannot imagine what mechanism means that one cold century is followed by another cold one unless it's that the drivers of century-scale changes only change slowly. i.e. Koutsoyiannis' rule is just another way of saying climate has changed slowly in the past. That may be true but it doesn't prove that the climate won't change quickly in future if CO2 AGW theories are true.
Re Justice4Rinka's point about coins, it may be that Koutsoyiannis is just describing a stochastic phenomenon, but I make the same point that saying the climate was stochastic before AGW says nothing about how it will behave if the drivers are no longer random. i.e. If AGW is a factor.
"Please, take care with statements on the Second Law of Thermodynamics. It is often misunderstood."
Fair comment Geoff, perhaps you can enlighten us all - as to the rest of the post, yes indeed and taken on board, as it were.
GISS, HadCRUt crib, borrow of GHCN record but this is not a complete or reliable data source.
How can we trust the T record?
Extrapolation, of dodgy figures is just sorcery, but drawing pessimistic conclusions about runaway global warming [+1.5 - 6 degrees this century!] and, that this 'warming' is induced by man made CO2 emissions - that is a correlation not made.
What we can say without equivocation is that, the temps since the recent little ice age have indeed risen, anecdotal evidence showing the growing season, then, Circa 1750 was considerably less than now in the northern hemisphere, wonderfully it has lengthened and hooray for that.
Temperature rises are cyclical and that we are in an interstitial warming between the last ice age retreat and the next ice advance.
Making bold assumptions about where the temperature will be in [even] 20 years is a shot in the dark, my guess is: that we are in for a considerable cooling phase, Icelandic/Chilean/world volcanic activity will aid further cooling and who can second guess anyone? The IPCC set great store in computer models and predictions as worthless as Mother Shipton's tea leaves.
The main point of the Realist position, is how can we force economic penury on the citizens - particularly in Britain, if the predictions are not worth the paper they're written on?
If this was purely an academic argument - I'd leave it well alone - but it isn't is it?
And, irrespective of knowing the ins and outs of the second law of thermodynamics, it's still a relatively free country - that's why I will remain a staunch critic of the madness of AGW.
To my untutored eye, there seems to be clear evidence that the land-based temperature record has been gerrymandered to the point where it is meaningless; the furore over this precise point in New Zealand is proof enough for me of the agenda that has become increasingly evident; control the past to control the future. Honest science doesn't seem to get much of a look-in in the strange and surreal world of Climate Science.
There is a preprint of the Koutsoyiannis paper here:
http://itia.ntua.gr/getfile/1102/1/documents/2011PhysicaA_HKfromExtremalEntropyProduction_pp.pdf
Is there an analogy here with Brownian diffusion? At small time scales density fluctuations are given by the standard diffusion equation. However at longer time scales a Fokker-Planck (or Smoluchowski) formalism generates a memory kernel that is dependent on past movements by the Brownian particles themselves (as well as other things). So at longer time scales the process becomes non-Markovian. The timescales are markedly different to those here of course, butthe physics of a particle's motion through a liquid affecting its motion at a later time makes sense.
However, with Julian, I would appreciate some sort of physics explanation of what appears to be this non-Markovian behaviour in the climate record.
About physical mechanisms, there are indeed some that could account for this. As an example, if a century were unusually cold, then glaciers might grow, and that would tend to cool the next century. As another example, some ocean waters sink below the surface and take centuries, or even millennia, to resurface; when they resurface, they carry some memory of the climate from when they sank. Climatic changes can also force changes in vegetation—e.g. desertification—that in turn modify the climate, thereby leading to long-term persistence of the climatic changes.
The paper does not address the issue of physical mechanisms for global temperatures, because it is really about any system for which the assumptions are reasonable. I.e. it is primarily a theoretical result.
It is not clear that the statistical model handles exogenous forcings, such as changes in solar radiation or volcanic eruptions. More generally, the formula would seem to be only an approximation. We do not know how good an approximation it is.
The formula, though, seems to be the best-fitting formula that is known for the global temperature series (as detailed in previous papers). A major puzzle was to understand how that could be true. By deriving the formula from more basic assumptions, which are plausible (though probably not exact), Koutsoyiannis seems to have resolved the puzzle.
GrantB, the behavior is Markovian, on all time scales.
Re Julian,
Think of coin flips where if its heads then the temp goes up by one unit and if its tails then it goes down by one.
You can easily see that in the short term then each years temp is influenced by the previous because it can only go up or down in a single step. But this relationship holds for century and millennium time scales (or coin flips).
Consider a starting point at normal temperature and flipping the coin to see if each years temp goes up or down.
After 100 coin flips he chances of getting exactly 50/50 split with heads and tails are only 0.08. The odds are you get between 40 and 60 heads (0.96 probability). If we assume we got 55 heads then the century was "warmer than normal".
The next century starts from this warmer position so the possible outcomes at the end of the second century are:
1. Normal temperature - exactly 45 heads required - probability of 0.05
2. Warmer temperature - More than 45 head required - probability of 0.82
3. Colder temperature - Less than 45 heads required - probability of 0.14
(rounding errors result in the probabilities adding up to 1.01)
You can see that the most likely outcome of the second century is that its warmer and that there is less than a one in seven chance or it ending up colder than normal.
In other words the second centuries temperature is related to the first centuries.
DISCLAIMER: Yes I know temperature changes aren't governed by a coin flip. Yes I know my coin flip climate model allows for both unbounded lower and upper temperatures.
@ peter2108
I think the inference one can draw is that the amount of data you have, three coin tosses, is not enough to tell you anything conclusive about which coin you drew. It also does not help you if what you are actually trying to find out is whether one of the coins is indeed biased. This for me is what Doug K set out rather well in the article he refers to.
@ Roger
It was indeed intentional, but I can't claim the credit for it. I think I first read it here. It seems to fit the bill quite well.
@ Julian
Fair point, but what's being suggested, I think, is that if you posit a stochastic nature to recent temperature trends, it explains them so convincingly that you wouldn't think to bring CO2 into it at all.
The bit of correlation I'd still like to see is the one that shows net CO2 emitted versus net atmospheric CO2. I'm aware of a rising component of fossil CO2 in the atmosphere, but not of any proven correlation between total atmospheric CO2 and human emissions of it.
This strikes me as being every bit as necessary as a temperature history in order to draw any inferences about human effects. Otherwise, we are in the position of a man adding water to a bath at a rate of a teaspoonful a day, and who is convinced that he will quite soon and inevitably flood the bathroom.
He might be right, but he can't possibly know either way unless he knows whether the bath plug is in.
As far as I know this hasn't actually been done, i.e. the accuracy of the estimates of CO2 emission are so wide that if the entire human part of it were to be over- or understated by 100% it wouldn't show up!
It seems clear to me that if you were to randomly pick one century from the past million years and then consider the centuries either side of it, they would be similar in terms temperature, mainly due to the degree of glaciation.
We don't seem to be very good at thinking in terms of hundreds, thousands or millions of years and sometimes have a tendency to assume that the conditions we first noticed are the "normal" ones and any change must be unnatural. The truth is that nature and climate were changing long before humans came along and will still be changing long after we're gone!
@Justice4Rinka
"...enough to tell you anything conclusive about which coin you drew." Agreed. Nothing conclusive. In the coin example Bayes tells you that the probability of the biased coin is .77 (hence of the unbiased one a mere .28). Not conclusive but enough for bets - and of course for "policy". Let's assume a mild "lukewarmer" view that doubling CO2 will lead to 0.75C warming. Does a warming trend provide no evidence at all in favour of that view? Would a clear cooling trend provide no evidence against it?
I wish to thank Doug Keenan for the post and all for the discussion.
I see a central question in the discussion is: What is the mechanism for this?
As an analogy, may I pose another question: What is the mechanism behind the ideal gas law? Of course, Newton’s 2nd law and the collision of gas molecules with the walls of the container of the gas are necessary elements to understand the law--the origin of pressure in particular. But these are not sufficient to derive the equation pV = nRT. The essential element that justifies the law is the entropy maximization. And, as discussed in the paper, entropy extremization is none other than the extremization of uncertainty.
Even Newton’s second law can be derived by extremization of action (principle of stationary action). So Nature is an extremizer.
For me entropy extremization--or, if we involve time, entropy production extremization--are sufficient physical explanations that make unnecessary additional mechanisms.
I think the idea that the Climate next (X) will be similar to the Climate last (X) [where (X) is a unit of time] has much to commend it.
We all probably know the junior school exercise where the accuracy of the yesterday's weather forcast is compared with the assumption that today's weather will be the same as yesterday's. And the latter prediction usually scores more highly than the 'scientific' weather forecast. (Particularly if it comes from Mystic Met.)
I guess that, for all sorts of reasons, a similar result might be achieved over longer time frames. It has been suggested many times that the Climate isn't entirely random and chaotic. Obviously, the Climate doesn't just 'wake up in the morning and decide what it fancies doing'. There are a myriad of processes going on, a few of which we have some real understanding, but all are likely dependant to some degree on the starting point.
This is certainly different to a coin toss. Whether or not the coin is biased, there is some chance that it will land 'heads', some similar chance that it will land 'tails' and preumably a far smaller chance that it will land balanced on edge or run down a mouse hole.
Whereas the possibilities for the weather in the next thousand years, or in the next decade, or in the next hour are almost infinitely more variable.
Douglas @Jun 6, 2011 at 1:14 PM - "GrantB, the behavior is Markovian, on all time scales".
Douglas, I haven't been involved with this for donkey's years although my thesis way back then was on non-Markovian (memory) effects in interacting suspensions. However from Wiki (sorry) a Markov process is
whereas you say "they carry some memory of the climate from when they sank". Surely you are referring then to a (physics defined) non-Markovian process. I realise that this is a statistical model and no one is proposing a Green's function for the memory kernel. I've always been impressed with Koutsoyiannis' work and if I could get away from my boring but well paid day job for long enough I'd like to get up to speed on it. Nevertheless an interesting paper.
Ah, Prof Koutsoyiannis, good to see that name come up! I'm quite busy at the moment but I'll see if I can answer one or two questions on my understanding of Prof K's work (of course be aware my understanding may not be the correct one!)
Firstly, assuming global temperatures exhibit Hurst-Kolmogorov (HK) behaviour, it would still be possible to detect an anomalous warming of some probability. It is just that, in comparison to classic (autoregressive) statistics, the confidence intervals are wider, and to achieve the same level of significance, we need a much larger warming. As Cohn and Lins have ably demonstrated, we have not yet reached that level.
Secondly, on the physical justification. This is a complex topic, and I'll give a "weak" answer and a "stronger" answer. The weak answer would be to ask what else do people think the natural variability is, and to observe the behaviour of temperature over a range of scales. The behaviour of temperature is visibly self-similar. Although this is a weak claim, it is an interesting thought experiment.
The variability of natural climate is, of course, enshrined in the complex (possibly chaotic) system which creates the climate. To determine the characteristics of natural variability is easy: just write out the equations, implement them in a numerical model, run the model, and look at the output. Of course, we fail this at the first hurdle, because we do not know the equations. So we cannot know what the true variability is. So to those who ask for a physical justification, one of my first questions is: how would you characterise natural variability, and what is your physical justification?
OK that is the weak answer. There is a strong case that Prof K has prepared for us, which is mentioned in the top post - maximum entropy. Prof K demonstrates from first principles that if we can apply certain constraints to a system, we can derive the type of variation that maximises entropy for non-negative time series. I am writing this from memory and may make mistakes:
If there is no serial correlation in a time series, entropy is maximised by "white noise" (IID).
If there is serial correlation in the time series, if the standard deviation is small with respect to the mean, and there is an explicit single time constant, entropy is maximised by "autoregressive noise" (STP, Markovian)
If there is serial correlation, no single preferred time constant, and the standard deviation is similar or larger than the mean, then entropy is maximised with "Hurst-Kolmogorov noise" (LTP)
I put noise in quotes, because these aren't truly "noise", but the trajectory of the complex system under analysis. But you all understand what I mean, right? For a more rigorous explanation of the above, see Prof K's docs.
For those who are paying attention, you may notice something. For temperature to be non-negative, it must be measured in Kelvin. It is serially correlated (temperature variations from minute to minute are small compared to day to day). But the standard deviation is small compared to the mean - it does not conform to the constraints above!
But if we look at cloud cover, we find it does conform. Cloud cover is non-negative. It is serially correlated (changing more day-to-day than minute-to-minute). And the standard deviation is high in comparison to the mean. (This is because cloud cover tends to be all or nothing; the time series contains lots of 0's, and a percentage of 1's, with 0's more likely, giving a standard deviation greater than the mean).
But cloud cover has a huge impact on temperature - locally and globally - as does other aspects of the hydrological cycle. The hydrological cycle imparts its HK behaviour - which is expected from first principles entropy maximisation - on to the global temperature series.
Now that is a strong argument for HK behaviour - especially when you consider two further things; firstly, that there is no strong case for the IPCC-preferred autoregressive noise, and secondly, when we look at ice cores, instrumental data and other proxies, we see scaling behaviour that is completely consistent with Prof K's findings.
So we have both a physical basis and observational evidence for HK behaviour in climate... but a reluctance of climate scientists to accept it.
Spence_UK, thanks very much for your penetrating explanations, and for being so kind (now and always).
Can I add a couple of notes for clarification. The level of variability (the relation between standard deviation and mean) is more relevant when we are interested about scaling properties *in state*, i.e. the marginal distribution function, and does not influence very much the *scaling in time*, i.e the dependence structure. Second (albeit not relevant to the first), the temperature (defined, in statistical thermodynamics, as the inverse derivative of entropy with respect to internal energy) *is* in fact a non-negative natural quantity (as is cloud cover, rainfall depth, etc). The fact that we use arbitrary scales like Celsius or Fahrenheit, which make a shift of origin, is irrelevant. Even the Kelvin scale is arbitrary (and unnecessary) as I write in the footnotes in the paper--but it is better than the others, as it respects the fact that temperature is non-negative. Of course, it does not change anything if we use these convenient scales, but we must be alert that, as a physical quantity, temperature is non-negative.
GrantB, to elaborate ... For any series X, “X(t+1) directly depends only on X(t)” is the same as “X(t) directly depends only on X(t−1)”.
GrantB:
How about a workshop in London some time, with Doug, Spence and Demetris?
...and this is why I am always cautious and include a disclaimer at the start of my posts!
Thank you for the clarifications and corrections Prof. Koutsoyiannis - the latter point makes complete sense, and is just my sloppy use of technical language. The former shows I had misunderstood a part of your analysis. I understand better now though, but it shows I need to read and understand your latest paper more carefully - I'm not happy unless I have the details completely straight in my mind!
Spence, I am flattered that you read my papers. You usually explain them better than I can do. I hope to discuss some time in person/public, perhaps in the workshop in London proposed by Richard.... or in a vacation in Greece...
Prof. Koutsoyiannis, thank you for your kind words, although I usually feel guilty for dragging you to all corners of the internet to defend your work! While I know I would learn a lot from such an opportunity I am wary of consuming even more of your time.
TAC over at ClimateAudit did almost persuade me to head along to the EGU assembly in Vienna one year, but the dates always clashed with my schedule, so I have not yet had the chance to visit.
London is convenient for me, and if the opportunity to travel through Athens arises, I would be happy to make a detour. I will send contact details so we can arrange something if the opportunity arises.
Hmmm yeah:
Maupertuis-ian minimalism is compelling indeed.
The present is a good intial condition for projecting the future.
As such the world is Markovian.
Markov is da man.
Just to mention that the UK Met Office view is that “it would be safer to assume that there is statistical independence between one winter and the next” – see:
http://www.thegwpf.org/science-news/2087-winter-resilience-a-met-office-advice.html
Of course this may be correct on a regional (rather than global) basis.
Re TimC
Comparing winter to winter breaks the contiguousness of the temperature series. You would be missing out the spring, summer and autumn (fall) seasons that separate the 2 winters.
Demetris, Spence: How can we in London compete with a vacation in Greece? :) But Doug's asked me for details of the idea by email and I hope we're going to kick it around a little.
I'm more of a believer in the importance of a deterministic approach to than statistical interpretations of physical systems, but when it comes to climate we really are dealing with random fluctuations coupled with some cyclic activity.
I am intrigued by the notions of Climate memory and Climate persistence. This to me makes GTA become redundant, it has no real meaning in assessing climatic changes because it is a picture of the past, not the recent past, not the present, nor the future.
Again we are left with the impression we know so very little about climate. The AGW hypothesis has a sound laboratory basis, but there is no empirical evidence to date that allows to us say that this hypothesis has any relevance to the behaviour of this planet's climate.
Richard, assuming that vacation in Greece is best during summer, what about planning something in London in winter? Actually, I will most probably be close to London next February.
Mac, I fully understand your sentiment - it is more intuitive to view science through the lens of determinism rather than statistical relationships. And, indeed, science traditionally progresses through the discovery of deterministic relationships.
It is also important to remember, though, that most deterministic relationships, when investigated in great detail, are typically found to have statistical underpinnings. Most deterministic relationships are simply the consequence of underlying statistical behaviour. But since science has generally progressed by finding the deterministic relationships first, it should make sense to do something similar with climate. Why try and run before we can walk?
The work by Prof. Koutsoyiannis, if correct, shows that nature has a little trick which, when it comes to climate, can easily catch out the unwary scientist. HK behaviour in climate means that when you look at a geophysical time series - whatever the length, whatever the scale - the series will tend to be dominated by low frequency components, with respect to the scale at which you are viewing it. These, in turn, mislead the viewer into seeing deterministic oscillations or perhaps correlations with other time series which are not true relationships, but an expression of unpredictable natural variability.
If this HK behaviour does exist, then concentrating on finding deterministic relationships will end up with never ending arguments over whose correlation looks best. Counter intuitively, for climate science, it may be more productive to study the underpinning statistics before looking for deterministic relationships.
That uproar from the clouds is the Gods laughing over their dice game.
===============
kim,
This is really great! You are a poet...
Great Heavens, thank you, D. I never expected to be one; I just got curious.
================
If you have a perfect model you do not need historic information.
Just the present state as initial conditions, and the complete PDEs should define the future.
If the model is flawed however and there are hidden variables around, then historic information can help to include them implicitely. That's when you need memory in the system.
So GCM that do not take the Ocean's calorific content into their model, and the Sun's furnace model they'll have to include the weather of the last 1000000 years in their computations.
One would have hoped that the recent subprime crisis would have reminded the scientifically literate that a computer model constructed during a particular part of a cycle cannot be relied upon to perform equally well in a different part of the cycle. Anybody believing claims about the predictions of a computer model that has only ever existed in a tiny section of a cycle - and using data from an equally small dataset - shouldn't be doing so with other people's money, particularly mine.
Just a note that I made referenced Doug Keenan's article along with comment about properties of AR1 models at Statistics and Climate – Part Three – Autocorrelation.